Autoencoder (part 1)

What is an autoencoder

An autoencoder is a deep neural network atchitecture that is used in unsupervised learning, it consists of three parts, an encoder, a decoder and a latent space. The goal of an autoencoder is to encode high dimensional data to a low dimensional subspace by means of feature learning.

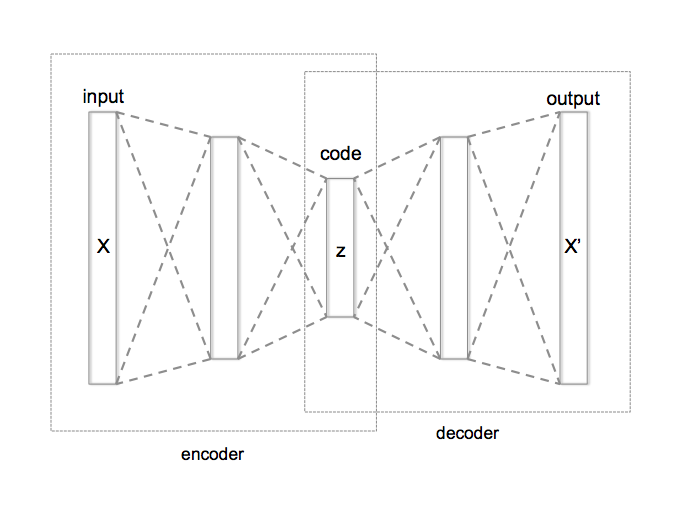
The formulation is as follows:

Given an input vector \( X \in \mathbb{R}^n \), the encoder $f:\mathbb{R}^n\rightarrow\mathbb{R}^m$ does the following

$$Z = f(X) \in \mathbb{R}^m$$

where $m\leq n$. In other words, the encoder compresses the input to a lower dimensional vector space called the “latent space”, correspondingly $Z$ is called the “latent reprepsentation” of the input $X$.

The decoder on the other hand, takes the latent vector $Z$ and tries to reconstruct the original input vector $X$. i.e

$$X^\prime = f^{-1}(Z) \in \mathbb{R}^n$$

So an autoencoder is essentially an approximation of the identity function on $\mathbb{R}^n$. The network is then trained to minimize the reconstruction loss of $X^\prime$. Often times it will be the mean-squared-error

$$l(X, X^\prime) = \frac{1}{n} \sum_{i=1}^n ||x_i - x^\prime_i||^2$$

Why autoencoder?

Data that appears in nature are usually very high dimensional but sparse, we know from experience that these data are not well suited to be used straight away for machine learning. By using an autoencoder as a dimenison reduction estimator, one can in theory compress these data into any desired dimension.

If the dimension of the latent space $m \in \{2, 3\}$, we can even visualize the latent space and get a glimse on the geometry of the data, which helps us understand our data even better.

More importantly, the latent space representation is dense, which means we can traverse along different trajectories within the latent space, and interpret the results through the decoder. One such example is linear interpolation between two points in the latent space.

Given input vector $X_1$, $X_2$ the line segment between latent vectors $Z_1$ and $Z_2$ is as follows

$$Z_t = Z_1(1-t) + Z_2\:t \quad t\in [0,1]$$

We can then interpret this equation through the decoder output

$$X^\prime_t = f^{-1}(Z_t) \quad t\in [0,1]$$

There’s just one more perk autoencoder brings to the table, it allows us to sample from the data’s distribution in the latent space and create more data, this is especially important if we are lacking in data quantity.

Implementation in Python with Keras

We will now build an autoencoder with Keras and demonstrate it with the MNIST dataset.

Notice the number of filters evolves in the way described above, the input dimension is 784 = 28 x 28 as we have flatten the image, the latent dimension is 2 for easy visualization of the latent space.

We will train the network for 100 epochs and use the testing data for validation, after training we will plot the loss and explore the latent space.

We can now see how the latent space structure looks like

Now linearly interpolate between any “zero” and “one” image in the latent space to see the decoded results

This technique is useful in places where knowing the intermediate steps between ends is important, like DNA seqeuncing or solving algebraic equations.

Drawbacks of autoencoders

Autoencoders could end up learning nothing but simply copy and paste the input as the output, this is the eventual destiny of any vanilla autoencoder, since it’s approximating the identity function; this will be harmful if our goal was to generate more data from our sample (time inefficient and quality deficient). Moreover, autoencoders trained this way are sensitive to the input, any distortion to the data (noise, rotation, reflection) could detriment the model’s ability to generate correct output.

Are there ways that we can ensure variety, stability and quality of the generated data in an autoencoder? Go to Other types of autoencoders to see more.