Categorical variables are discrete variables that take values from a finite set. Examples of some categorical variables are
- Blood type: A, B, C
- Countries: France, England
- The ranking of an NBA team: 1, 2, 3
While some machine learning algorithms can use these variables directly (tree based algorithms), most algorithms can’t handle non-numeric variables. It is then necessary to transform them to numerical variables if we were to use these algorithms.
Label encoding and One-hot encoding
Label encoding is the act of randomly assigning integer values to categories. E.g
Blood type - A:1, B:2, AB:3
While this encoding scheme solves part of the problem, they introduce numerical structures that are not apparent in the original variable. For instance, we see that an ordering of blood type has emerged $A<B<AB$, moreover airthmetic can now be performed
So the average of all blood types is $B$, which does not seem very sensical. Also, the order can be randomly permuted so that our little example above could essentialy give non-unique answers. Which is undesirable.
One-hot encoding converts each category to a binary variable, where a 1 indicates that the sample belongs to that category and 0 otherwise. For example, if we have three categories $cat, dog, mouse$, then
| dog | cat | mouse | |
|---|---|---|---|
| dog | 1 | 0 | 0 |
| mouse | 0 | 0 | 1 |
This is both very easy to understand and effective when the number of categories is not too much. However, if we have 10000 different categories, then it becomes problematic, namely we will encounter the curse of dimensionality and memory issues. For a 10000 category, the total number of combinations is $2^{10000}$, which is a huge number. For a single decision tree covering all these combinations, this is the number of leaves in the tree. You can imagine how long it will take to learn even the easiest pattern, and so the algorithm might choose to only learn the basic patterns such as random guessing by class probability etc.
The problem
Our main problems are the high dimensionality and undesirable arithmetic strucutre brought by these encoding methods. Is there a way that we can reduce these dimensions while not introducing arithematics that don’t make sense?
Target encoding
Target encoding [1] is a method of converting categorical variables to a numerical variable using information from the target variable (if it’s available). So the output will be a single vector instead of a matrix, our high dimensionality problem would have been averted if this works.
The details are quite simple to understand actually. Given $x=c$ where $c$ is a category with $n$ number of samples, the encoding for $x$ is given by
is a monotonically increasing function.
Let me explain what’s happening, we want to encode the category $c$ by the class mean/prboability, this is given by the quantities and $\Pr(y \mid x)$. This is the posterior distribution that we are estimating from the samples provided, when the per class sample size is small, the estimation diffiates from the true posterior distribution, which would give incorrect information about the class and introduce noise to the variable overall.
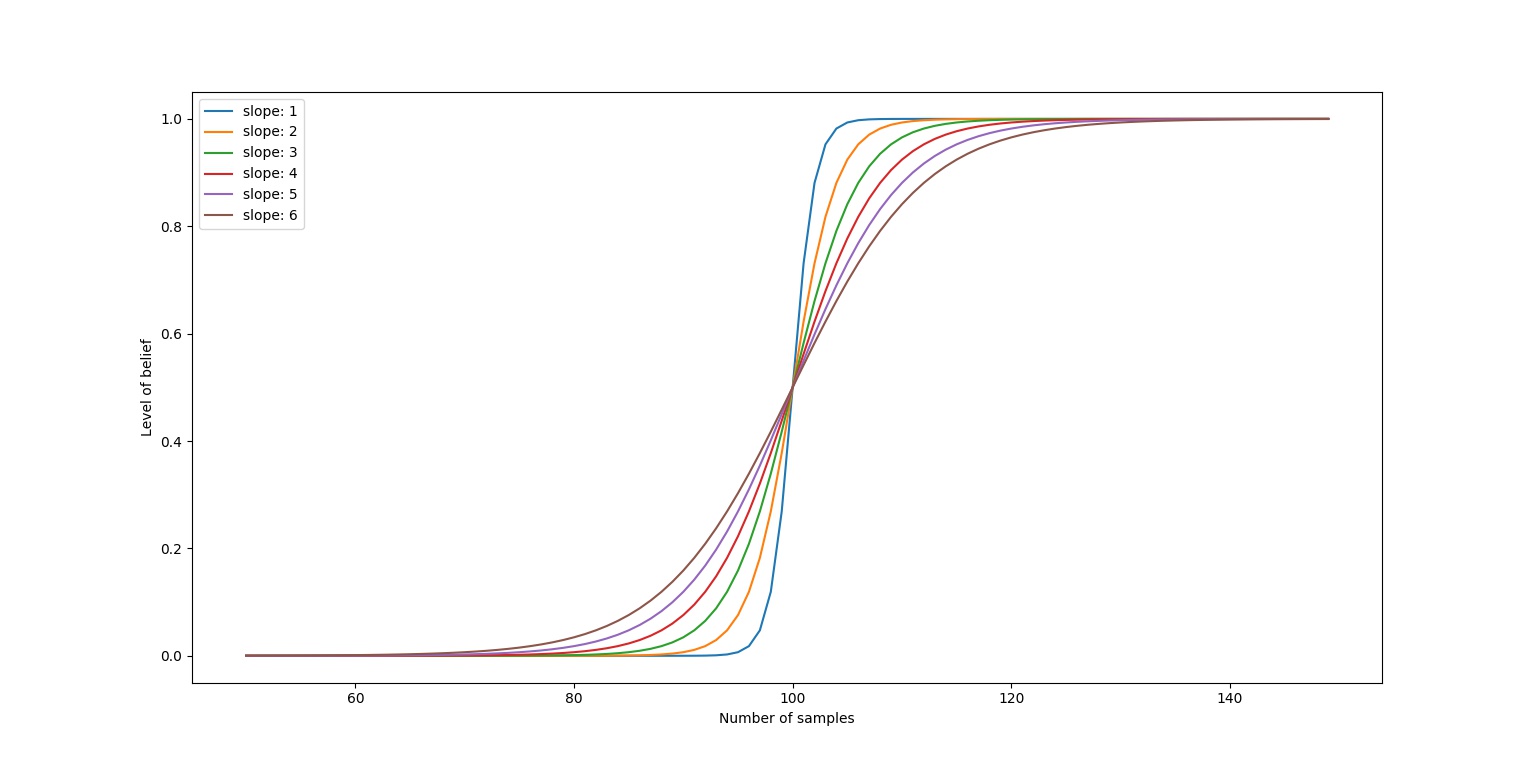
Instead, we include a level of belief called $\lambda$ between the estimated posterior and the sample prior $\Pr(y)$/$\mathbb{E}[y]$. The methodology here is, the more sample of category $c$ we can get, the more we beileve in the estimated posterior, so $\lambda$ must be monotonically increasing.
There are many choices of $\lambda$ one can choose. However, the chosen function should be reflective of the data size one’s currently working with. A $\lambda$ was suggested by Micci-Barreca in his paper[1].
$k$ is known as the “threshold” and $f$ is a smoothing parameter that determines the “slope” of the function around $k$. If $f\rightarrow \infty$, $\lambda$ basically becomes a hard-thresholding.
What about the bias bro?
Now, including information from the target variable sounds all kinds of wrong in the world of machine learning, as it would cause overfitting if not done carefully. Moreover, when applied to testing data, there are no labels provided, so how do we cope that situation?
Those are all legit concerns, one way to overcome all of these issues is to use “cross-validation”. I put it in quotes because we are not actually evaluating the score of a model, we simply want to use the methodology of cross-validation to reduce bias built up by using target encoding.
Cross-validation in target encoding
The idea is as follows
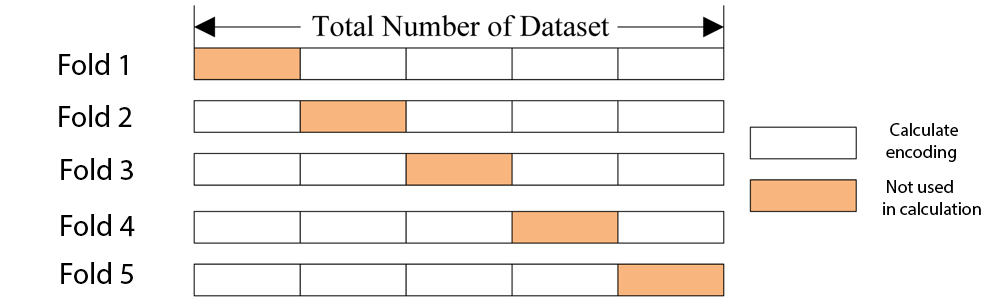
In practice, the training set inside each fold is further divided into more folds to include more noise to the encoding of each class (some noise is preferred here as it adds diversity to each class without tempering too much with the actual statistics).
The implementation is as follows
(The code only works for a pandas dataframe now, if you have a suggestion to optimize this code or extend it to non-dataframe type objects. Please let me know!)
Entity embedding
If you are a Kaggler like me, you would have discovered early on that neural networks don’t work great on Kaggle problems. This is because categorical data don’t have an apparent continuity built into them, and neural networks are only great at approximating continuous/piece-wise continuous functions.
Using one-hot encoding or target encoding can essentially avert this problem. However, as we noted before, one-hot encoding introduces excess dimensions and target encoding only takes the impact of the category towards the target into account.
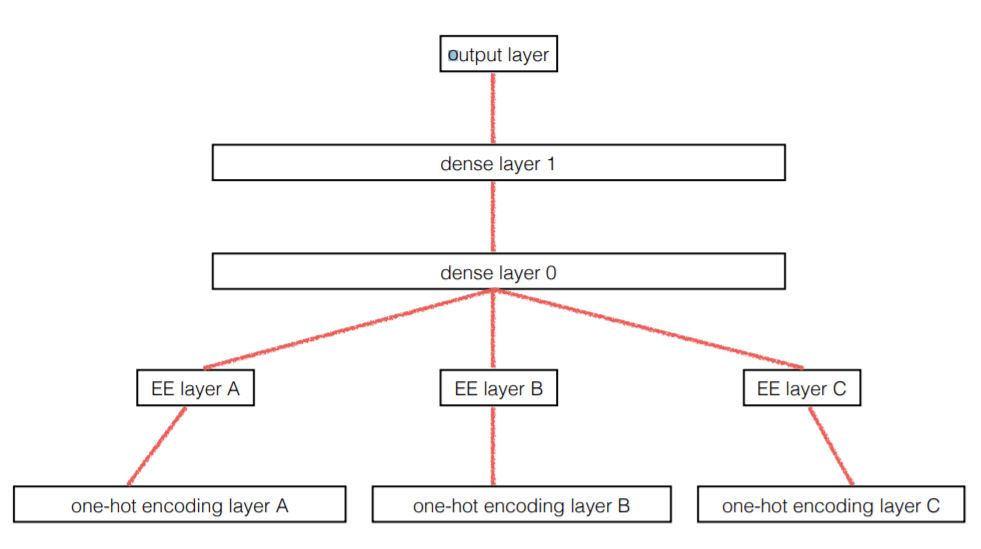
We will explore a method known as Entity embedding [2], which uses a neural network to learn an embedding for each categorical variable.
The overall structure is as follows
The first layer is called the embedding layer, all categorical variables are converted into a one-hot vector $\delta_{x_i\alpha}$, it is then fed into a fully connected layer, whose weights will be treated as our embedding. So the output of our embedding layer looks like this
$\beta$ is the embedding lookup index.
After the embedding layer, the output vectors are concatenated with continuous variables from the dataset, further feedforward network is then included. The output of this model is the prediction $\hat{y}$, weights can be updated via backpropagation minimizing an appropriate loss function (log loss for classification, MSE for regression etc.)
Below is an implementation in keras.
Some thoughts…
Extending target encoding
In our formula above, we have used the $\mathbb{E}(y\mid x)$ and $\Pr(y\mid x)$. We could include more variables than just $x$ when we encode. For instance, if $X = {x_1, \dots, x_n}$ are categorical variables, we can instead choose to do
where $A \subseteq X$ is a subset of $X$. So in a sense, this is including “interactions” between the variates. One could argue that, when encoding this way, we can combine the variables in $A$ into one variable. But I don’t have proof or experimental evidence to support that… (This is left for future work)
Why should entity embeddings be learned supervised..?
In other areas such as NLP and facial recognition, embeddings aren’t acquired this way. Specifically, embeddings are learned by exploting the internal structure of the features within a dataset, not by its impact on a target variable. So these embeddings/encodings are learned by means of unsupervised learning (Word2Vec, FastText, PCA, Autoencoder, etc.).
The approaches we have introduced are all problem specific, meaning the embeddings/encodings learned are likely not ready to be reused in a different set of problem (with the potential exception of entitiy embedding). Perhaps one could generalize the architectures to allow unsupervised learning in categorical embeddings too, we shall explore more on this in part 2…